Question

The triangle below is equilateral. Find the length of side a in simplest radical form

with a rational denominator.
X
√6

Answer 1

Check the picture below.

since the triangle is equilateral, is also equiangular.

`a√(3)=√(6)\implies a=\cfrac{√(6)}{√(3)}\implies a=\cfrac{√(2\cdot 3)}{√(3)}\implies a=\cfrac{√(2)√(3)}{√(3)}\implies a=√(3) \\\\[-0.35em] ~\dotfill\\\\ 2a=x\implies {\Large \begin{array}{llll} 2√(3)=x \end{array}}`

Answer 2

In an equilateral triangle with a height of
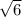`\(√(6)\)` and one side measuring x, the length of side x is
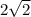`\(2√(2)\)` in simplest radical form with a rational denominator.

In an equilateral triangle, the height (h) can be related to the side length (x) using the Pythagorean theorem. The formula is:

`\[ h^2 + \left((x)/(2)\right)^2 = x^2 \]`

Given that the height is
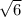`\( √(6) \)`, substitute
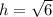`\( h = √(6) \)` into the equation:

`\[ (√(6))^2 + \left((x)/(2)\right)^2 = x^2 \]\[ 6 + (x^2)/(4) = x^2 \]`

Now, solve for x:

`\[ (3x^2)/(4) = 6 \]\[ x^2 = (24)/(3) \]\[ x^2 = 8 \]\[ x = √(8) \]\[ x = 2√(2) \]`

Therefore, the length of side x in simplest radical form with a rational denominator is
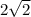`\( 2√(2) \)`.