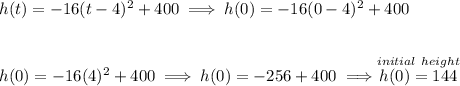Question

A given projectile has a height function given by h(t)=-16(t-4)^2+400. what is its maximum height and at what time, t, does it occur?

Answer 1

Check the picture below.

well, since h(t) is already in vertex form, well hell we pretty much can see the vertex right off

`~~~~~~\textit{vertical parabola vertex form} \\\\ y=a(x- h)^2+ k\qquad \begin{cases} \stackrel{vertex}{(h,k)}\\\\ \stackrel{`

now, when does it start above the ground?

well, from the picture below, notice, the initial height happens at 0 seconds, namely when t = 0, well, let's set it to 0.

`h(t)=-16(t-4)^2 + 400\implies h(0)=-16(0-4)^2 + 400 \\\\\\ h(0)=-16(4)^2 + 400\implies h(0)=-256+400\implies \stackrel{initial~height}{h(0)=144}`