Question

Becky is offered the two deals below.

Deal 1: She will get a quarter on the first day of the week. Each day thereafter for one week, she will receive double what she received on the previous day.
Deal 2: She will get $4 each day for 1 week. Which statement is true in every aspect regarding these two deals?

She should go with deal 1 because mc026-1.jpg is greater than mc026-2.jpg by $3.75.
She should go with deal 1 because mc026-3.jpg is greater than mc026-4.jpg by $35.50.
She should go with deal 2 becausemc026-5.jpg is greater than mc026-6.jpg by $27.33.
She should go with deal 2 because mc026-7.jpg is greater than mc026-8.jpg by $48.50.

Answer 1

A. She should go with deal 1 because (deal one equation here) is greater than by $3.75.

Answer 2

She should go with Deal 1 because Deal 1 is greater than Deal 2 by $3.75.

We can represent Deal 1 as a geometric sequence:

`g_n=0.25(2)^(n-1)`

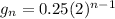
The 0.25 is the first term, 2 is the common ratio (it doubles every day) and n is the term number.

To find the total amount of money for this, we would find the sum:

`\Sigma_(n=1)^7(0.25)(2)^(n-1)`

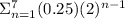
When we evaluate this sum, we get 31.75.

Deal 2 can be represented as 4(7) = 28.

This makes Deal 1 31.75-28=3.75 larger than Deal 2.