Question

An airplane flies eastward and always accelerates at a constant rate. At one position along its path, it has a velocity of 34.5 m/s . It then flies a further distance of 46100 m , and afterwards, its velocity is 40.7 m/s . Find the airplane's acceleration.

Answer 1

the acceleration of the airplane is 5.06 x 10⁻³ m/s²

Step-by-step explanation:

Given;

initial velocity of the airplane. u = 34.5 m/s

distance traveled by the airplane, s = 46,100 m

final velocity of the airplane, v = 40.7 m/s

The acceleration of the airplane is calculated from the following kinematic equation;

v² = u² + 2as

`2as= v^2 - u^2\\\\a = (v^2 - u^2)/(2s) \\\\a = ((40.7)^2 -(34.5)^2)/(2 * 46,100) \\\\a = 5.06 \ * \ 10^(-3) \ m/s^2`

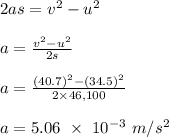
Therefore, the acceleration of the airplane is 5.06 x 10⁻³ m/s²