Question

Two charged particles, with charges q1=qq1=q and q2=4qq2=4q, are located on the x axis separated by a distance of 2.00cm2.00cm . A third charged particle, with charge q3=qq3=q, is placed on the x axis such that the magnitude of the force that charge 1 exerts on charge 3 is equal to the force that charge 2 exerts on charge 3.Find the position of charge 3 when qqq = 2.00 nCnC .

Answer 1

Answer: Charge 3 is located on the x-axis a distance of 0.67 cm from charge 1 and 1.33 cm from charge 2.

Step-by-step explanation: Electrostatic Force is the force of repulsion or attraction between two charged particles. It's directly proportional to the charge of the particles and inversely proportional to the distance between them:

`F=k(|q||Q|)/(r^(2))`

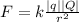
k is an electrostatic constant

For the system of 3 particles, suppose distance from 1 to 3 is x meters, so, distance from 2 to 3 is (0.02-x) meters.

Force will be

`F_(13)=F_(23)`

`k(q_(1)q_(3))/(r_(13)^(2)) =k(q_(2)q_(3))/(r_(23)^(2))`

`(q_(1))/(r_(13)^(2)) =\frac{q_(2)}{r^(2)_{{23}}}`

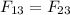
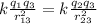
Substituting:

`(2.10^(-6))/(x^(2)) =(8.10^(-6))/((0.02-x)^(2))`

`8.10^(-6)x^(2)=2.10^(-6)(0.0004-0.04x+x^(2))`

`4x^(2)=x^(2)-0.04x+0.0004`

`3x^(2)+0.04x-0.0004=0`

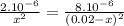
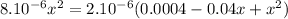
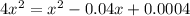
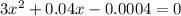
Solving quadratic equation using Bhaskara:

`x_(1)=\frac{-0.04+\sqrt{(0.04)^(2)+0.048} }{6}`

`x_(2)=\frac{-0.04-\sqrt{(0.04)^(2)+0.048} }{6}`

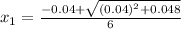
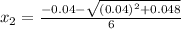
x₂ will give a negative value and since distance can't be negative, use x₁

`x_(1)=(-0.04+√(0.0064) )/(6)`

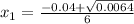
x₁ = 0.0067 m

The position of charge 3 is 0.67 cm from charge 1 and 1.33 cm from charge 2.