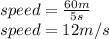Question

An astronaut drops a rock into a crater on the moon. The distance, d(t), in meters, the rock travels after t seconds can be modeled by the function d(t)=0.8t^2 . What is the average speed, in meters per second, of the rock between 5 and 10 seconds after it was dropped?

Answer 1

Plug in 5 and 10 to the equation.

For the first one would be d(5)=0.8(5)^2. Multiply the equation, d(5)=4^2. Then you just multiply the exponent and the answer would be, d(5)= 10

The second one, you just do the same thing and the answer would be d(10)= 64

Answer 2

12m/s

Explanation:

The distance is given by the function:

`d(t)=0.8t^2`

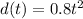
the distance at 5 seconds is:

`d(5)=0.8(5)^2\\d(5)=0.8(25)\\d(5)=20m`

and the distance at 10 seconds:

`d(10)=0.8(10)^2\\d(10)=0.8(100)\\d(10)=80m`

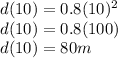
So, the distance covered in the interval of time between 5 and 10 seconds is:

`distance=d(10)-d(5)\\distance=80m-20m\\distance=60m`

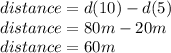
All of this is done to find the average speed with the formula:

`Speed=(distance)/(time)`

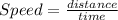
and we substitute the distance covered wich is 60m, and the time between 5 and 10 seconds which is 5 seconds.

the average speed is:

`speed=(60m)/(5s)\\ speed=12m/s`