Question

Which graph represents the function f(x)=5-5x2/x2?

Answer 1

I first assumed that you meant

5(1-x^2)
f(x)=5-5x2/x2 = > f(x) = --------------
x^2.

If I were now to let x grow large without bound, the function value would approach -5. This would be true coming from either direction, right or left. Thus, if my interpretation is correct, the 2nd graph is likeliest to be correct.

Answer 2

Note: When degrees of top and bottom are same, the Horizontal asymptote would be the ratio of leading coefficients of top and bottom.Given rational function: f(x) =
`(5-5x^2)/(x^2)`.

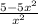We need to explain, which graph is correct graph for the given rational function.

Let us find some properties for the given rational function: f(x) =
`(5-5x^2)/(x^2)`.

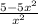Let us find vertical asymptote first.

In order to find vertical asymptote, we need to set denominator expression equal to 0 and solve for x.

Therefore

x^2 =0

x =0.

Therefore, vertical asymptote is at x=0.

Let us find Horizontal asymptote now.

We have leading coefficient of top is -5 and leading coefficient of bottom is 1.

Therefore, Horizontal asymptote would be y = -5/1 or y = -5.

Let us find the graph with vertical asymptote at x=0 and Horizontal Asymptote y =-5.

Therefore, graph in second option is correct graph which has Vertical asymptote at x=0 and Horizontal Asymptote y =-5.