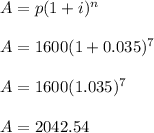Question

If you can show your work so I can learn that would be great (all three questions go together). If you have any questions please ask

1. You and your best friend want to take a vacation to Peru. You have done some research and discovered that it will cost $2400 for the plane tickets, all-inclusive hotel and resort, and souvenirs. You have already saved $1750. If you invest this money in a savings account with a 2.3% interest rate compounded annually, how long will it take to earn enough money to go on the trip? Use the compound interest formula A = P (1 + i)n, where A is the accumulated amount, P is the principal, i is the interest rate per year, and n is the number of years. Round your final answer to the nearest tenth

2. You are planning to go on this trip in 2 years. How much money will you need to invest at a 2.3% interest rate compounded annually in order to have $2400 in 2 years? Use the compound interest formula A = P (1 + i)n. (Round final answer to the nearest cent, but otherwise don’t round any intermediate values)

3. Now say you only have $1600 to invest and the highest interest rate you can find is 3.55% compounded annually. If you decide to wait 7 years to go on the trip, how much money will you have to spend on the trip? Use the compound interest formula A = P (1 + i)n. (Round final answer to the nearest cent, but otherwise don’t round any intermediate values)

Answer 1

1) 13.9 years
2) $2293.30
3) $2042.54

Step-by-step explanation:
1) Using the equation

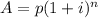
`A=p(1+i)^n`, plugging in our values, we have:


`2400=1750(1+0.023)^n \\ \\2400=1750(1.023)^n \\ \\(2400)/(1750)=1.023^n`

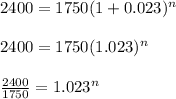
Using logarithms to solve this, we have:

`\log_(1.023)((2400)/(1750))=n \\ \\13.9=n`

2) This time, we substitute different values into our equation:

`A=p(1+i)^n \\ \\2400=p(1+0.023)^2 \\ \\2400=p(1.023)^2 \\ \\(2400)/(1.023^2)=p \\ \\2293.30 = p`

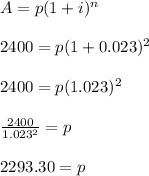
3) This time we change all of the values in our equation:

`A=p(1+i)^n \\ \\A=1600(1+0.035)^7 \\ \\A=1600(1.035)^7 \\ \\A=2042.54`