Question

Which choice is equivalent to the expression below?

2^8.24

A. 2^8+2^2/10+2^4/100
B.2^8*2^2/10*2^4/100
C. 2^8*2^24/10
D.2^8+2/10+4/10

Answer 1

B is your answer because if you check each one in the calculator B is the same as the expression and also 2^8 makes up the first part and the second half makes up the .24

Answer 2

`2^(8)\cdot 2^{(2)/(10)}\cdot 2^{(4)/(100)}`

B is correct

Explanation:

Given:
`2^(8.24)`

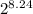
Using exponent law,

`x^(a+b)=x^a\cdot x^b`

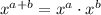
Expand exponent 8.24

Position of each digit:

8 ⇒ It is at tens place (1 x 8)

2 ⇒ It is at tenth place (1/10 x 2)

4 ⇒ It is at hundredth place (1/100 x 4 )

`8.24=8+.2+.04`

`8.24=8+(2)/(10)+(4)/(100)`

`2^(8.24)=2^{8+(2)/(10)+(4)/(100)}`

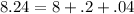
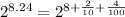
Using exponent law

`2^(8.24)=2^(8)\cdot 2^{(2)/(10)}\cdot 2^{(4)/(100)}`

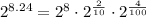
Hence, The equivalent expression is
`2^(8)\cdot 2^{(2)/(10)}\cdot 2^{(4)/(100)}`