Answer:
For 10.0 mL, pH=9.81
For 20.0 mL, pH=5.42
For 30.0 mL, pH=1.41
Step-by-step explanation:
Hello,
At first, the undergoing chemical reaction is:
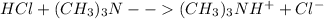
Nevertheless, once the acid added but before the equivalent point, the trimethylamine reacts with the dissociated hydrogen ions provided by the hydrochloric acid as shown below:
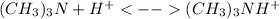
A) 10 mL of HCl
In this manner, the fist addition of 10 mL HCl leads to the following pH calculation:
Before the reaction:
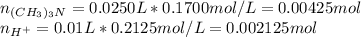
After the reaction:

Now, the conversely chemical reaction (
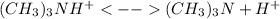 ) defines the pH via the equilibrium law of mass action calculation:
) defines the pH via the equilibrium law of mass action calculation:
![Ka=([H^+]_(eq)[(CH_3)_3N]_(eq))/([(CH_3)_3NH^+]_(eq))](https://img.qammunity.org/2019/formulas/chemistry/college/64bktzaqcxjac5canw7r1tu3ouy7axpbe4.png)
Ka is computed via:
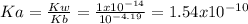
Now, defining
 as the concentration change during the chemical reaction, its value will account for the concentration of hydrogen which subsequently allows us to compute the pH considering that the initial concentrations match with the concentrations after the addition of the 10mL of HCl, thus:
as the concentration change during the chemical reaction, its value will account for the concentration of hydrogen which subsequently allows us to compute the pH considering that the initial concentrations match with the concentrations after the addition of the 10mL of HCl, thus:
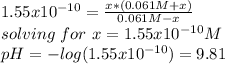
B) Now, after 20 mL have been added we obtain:
Before the reaction:
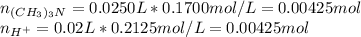
After the reaction:

By applying the same previous procedure, the pH is then:
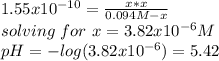
(here is the equivalence point).
C) Finally, after 30.0mL have added:
Before the reaction:
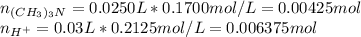
After the reaction:
![M_((CH_3)_3N)=(0.00425mol-0.00425mol)/(0.025L+0.03L) =0M\\M_(H^+)=(0.006375mol-0.00425mol)/(0.025L+0.03L) =0.0386M</p><p>In this case, the concentration of hydrogen in excess, 0.0386M is just enough to compute the pH since all of the base is consumed, thus:</p><p>[tex]pH=-log(0.0386)=1.41]()
Best regards.