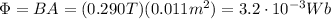Question

A circular area with a radius of 6.00 cm lies in the xy-plane. part a what is the magnitude of the magnetic flux through this circle due to a uniform magnetic field with a magnitude of 0.290 t in the + z -direction?

Answer 1

The magnetic flux through an area A is given by

`\Phi = BA \cos \theta`
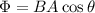
where
B is the magnitude of the magnetic field
A is the area

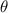
`\theta` is the angle between the direction of B and the perpendicular to the surface A.

In our problem, the area lies in the x-y plane, while B is in the z direction, this means that B and the perpendicular to A are parallel, so
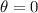
`\theta=0` and
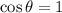
`\cos \theta=1`, so we can rewrite the formula as

`\Phi = BA`

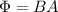
We can calculate the area starting from the radius:

`A= \pi r^2 = \pi (0.06 m)^2 = 0.011 m^2`
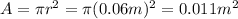
And then using the intensity of the magnetic field given by the problem,
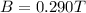
`B=0.290 T`, we find the magnetic flux:

`\Phi = BA=(0.290 T)(0.011 m^2)=3.2 \cdot 10^(-3)Wb`