Question

Select the inequalities represented by the graph below. Select all that apply.

Answer 1

A

Explanation:

Answer 2

`2x+y\geq c`

`y\geq -2x+c`

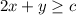
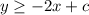
Explanation:

we know that

The solution of the inequality of the graph is the shaded area above the solid line

The slope of the solid line is negative

The y-intercept of the solid line is the point
`(0,c)`

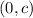
therefore

The inequalities represented by the graph are

case 1)
`2x+y\geq c`

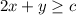
isolate the variable y

`y\geq -2x+c`

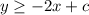
The solution of this inequality is the shaded area above the solid line

The slope of the solid line is negative
`m=-2`

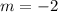
The y-intercept of the solid line is the point
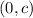`(0,c)` (value of y when the value of x is equal to zero)

case 2)
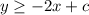`y\geq -2x+c` ------> idem case 1)