Alright, so, I'm so happy cause I got 100%, but this is how you solve the problem.
Since we have the info, here's the formula for it:
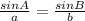
Since it doesn't have ΔABC, We'll use the acronyms of their names to make it easier. ΔMBK. We're solving for the length of K to M.
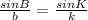
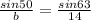
The substitutions for these are the numbers that represent them and the b is the length between K and M.
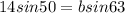
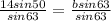
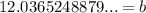
b = 12.0
Hope this helps you. :D