Question

In a survey of 200 people, 37% had a son, 31% had a daughter, and 23% had both a son and a daughter. What is the conditional probability that a person who has a son also has a daughter? Round to the nearest whole number.

Answer 1

About 46 people because that is 23% of 200

Answer 2

Answer: The conditional probability that a person who has a son also has a daughter is 62%.

Explanation:

Since we have given that

Total number of people = 200

Let A be the event having son.

Let B be the event having daughter.

P(A) = 37%

P(B) = 31%

P(A∩B) = 23%

We would use "Conditional Probability" in which we have given that he has a son, and he now also has a daughter.

`P(B\mid A)=(P(A\cap B))/(P(A))\\\\P(B\mid A)=(23)/(37)\\\\P(B\mid A)=0.62\\\\P(B\mid A)=62\%`

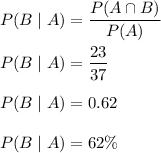
Hence, the conditional probability that a person who has a son also has a daughter is 62%.