Question

A cube has an edge length of 6 cm. It is to be enlarged by a scale factor of 4. What is the surface area ratio of the enlarged cube to the original cube? Enter your answer, as a fraction in simplest form, in the box\

Answer 1

16/1

Explanation:

Answer 2

The surface area ratio of the enlarged cube to the original cube is 16:1, or as a fraction, 16/1.

If the scale factor is 4, the edge length of the enlarged cube is 24 cm.
(6 × 4 = 24)

To find the surface area of a cube, you can use the formula
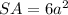
`SA=6a^2`, where a is equal to the edge length of the cube.

First, I will solve for the surface area of the original cube.

SA = 6 × 6²
SA = 6 × 36
SA = 216

Next, I will solve for the surface area of the enlarged cube.

SA = 6 × 24²
SA = 6 × 576
SA = 3456

To find the ratio, we divide the original cube's surface area from the enlarged cube's surface area.

3456 ÷ 216 = 16

The surface area ratio of the enlarged cube to the original cube is 16:1, or as a fraction, 16/1.