To solve this we are going to use the speed equation:
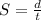
where
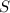
is speed

is distance

is time
First, we are going to label the information that the problem is giving us:
Since the plane has enough fuel for a five our flight, the total time of the round trip will be five hours; therefore,
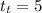
. We know that the speed of the plane with the wind is 225 miles per hour, so
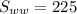
. We also know that the speed of the plane against the wind is 180 miles per hour, so

. Notice that Since we are dealing with a round trip, the distance against the wind and the distance with the wind will be the same.
For the trip with the wind:
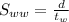
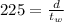
equation (1)
For the trip against the wind:
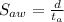
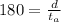
equation (2)
Since the whole trip takes 5 hours,
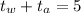
Solving for
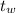
:
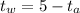
equation (3)
Replacing (3) in (1):
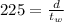
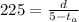
equation (4)
Solving for

in (2)
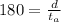

equation (5)
Replacing (5) in (4):
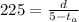
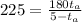
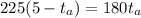
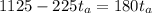

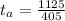

equation (6)
Replacing (6) in (5):

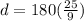
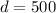
miles
We can conclude that the plane can travel a distance of 500 miles to make a round trip if it has just enough fuel for a five hour flight.