Question

A ball is projected in to the air. Its height at time t is given by the equation

h = -16t^2 + 60t + 1.
Solve for the time as which the height will be 8 feet. Show your work and explain the steps you used to solve. Round your answer to the nearest hundredth.

Answer 1

The equation gives the height of the ball. That is, h is the height of the ball. t is the time. Since we are looking for the time at which the height is 8 (h=8), we need to set the equation equal to 8 and solve for t. We do this as follows:


`h=-16 t^(2) +60t+1`

`8=-16 t^(2) +60t+1`

`16 t^(2) -60t-1+8=0`

`16 t^(2) -60t+7=0`

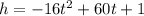
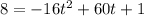
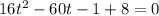
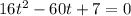
This is a quadratic equation and as it is set equal to 0 we can solve it using the quadratic formula. That formula is:

`t= \frac{-bplus minus \sqrt{ b^(2)-4ac } }{2a}`
You might recall seeing this as "x=..." but since our equation is in terms of t we use "t-=..."

In order to use the formula we need to identify a, b and c.
a = the coefficient (number in front of)
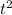
`t^(2)` = 16.
b = the coefficient of t = -60
c = the constant (the number that is by itself) = 7

Substituting these into the quadratic formula gives us:

`t= \frac{-(-60)plus minus \sqrt{ (-60)^(2)-4(16)(7) } }{2(16)}`

`t= (60plus minus √(3600-448 ) )/(32)`

`t= (60plus minus √(3152 ) )/(32)`

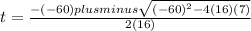
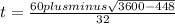
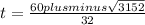
As we have "plus minus" (this is usually written in symbols with a plus sign over a minus sign) we split the equation in two and obtain:

`t= (60+56.1426)/(32) =3.63`
and

`t= (60-56.1426)/(32) =.12`

So the height is 8 feet at t = 3.63 and t=.12

It should make sense that there are two times. The ball goes up, reaches it's highest height and then comes back down. As such the height will be 8 at some point on the way up and also at some point on the way down.