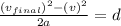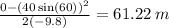Question

An ideal projectile lunched with angle 60 above the ground and initial velocity 40 m/s. Find the maximum height of this projectile. (g = 9.8m/s2)

Answer 1

Step-by-step explanation:

The maximum height of the projectile occurs when the velocity in the vertical direction is 0.

we know

`v = 40`

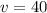
and that

`\alpha = 60 \: above \: the \: horizontial`

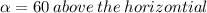
Since we have a magnitude vector and an direction angle, we need to break this vector up into components.

`v _(x) = 40 \cos(60)`

`v _(y) = 40 \sin(60)`

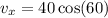
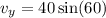
Next, we know g is

`a = - 9.8`

and our

`v log_(yfinal) = 0`

We know to find d, the vertical height.

Using our kinematic equations, we can use

`(v _(final)) {}^(2) = v {}^(2) + 2a(d)`

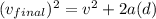
Since we referring to the y direction, our subscripts will be y.

First, isolate the quantity, d, and plug in knowns

`\frac{(v _(final)) {}^(2) - (v) {}^(2) }{2a} = d`

`\frac{0 - (40 \sin(60)) {}^(2) }{2( - 9.8)} = 61.22 \: m`