Question

Bradley and Kelly are out flying kites at a park one afternoon. A model of Bradley and Kelly's kites are shown below on the coordinate plane as kites BRAD and KELY, respectively:

Kite BRAD has the following coordinates: B is at point 3,7; R is at 4, 6; A is at point 3, 3; D is at point 2, 6. Kite KELY has the following coordinates: K is at point 11, 2; E is at point 9, 0; L is at point 3, 2; Y is at point 9,4.

Which statement is correct about the two kites?

A. They are similar because the corresponding sides of kites KELY and BRAD all have the relationship 1:2.
B. They are not similar because the corresponding sides of kites KELY and BRAD all have the relationship 1:2.
C. They are similar because the corresponding sides of kites KELY and BRAD all have the relationship 2:1.
D. They are not similar because the corresponding sides of kites KELY and BRAD all have the relationship 2:1.

I think C because it says KELY and BRAD, not BRAD and KELY. I also know that they are similar. Let me know if I'm correct.

Answer 1

The correct answer is:

C. They are similar because the corresponding sides of kites KELY and BRAD all have the relationship 2:1.

Using the distance formula,

`d=√((y_2-y_1)^2+(x_2-x_1)^2)`

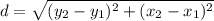
the lengths of the sides of BRAD are:

`\text{BR}=√((7-6)^2+(3-4)^2)=√(1^2+(-1)^2)=√(1+1)=√(2)</p><p>\\</p><p>\\\text{RA}=√((6-3)^2+(4-3)^2)=√(3^2+1^2)=√(9+1)=√(10)</p><p>\\</p><p>\\\text{AD}=√((3-6)^2+(3-2)^2)=√((-3)^2+1^2)=√(9+1)=√(10)</p><p>\\</p><p>\\\text{DB}=√((6-7)^2+(2-3)^2)=√((-1)^2+(-1)^2)=√(1+1)=√(2)`

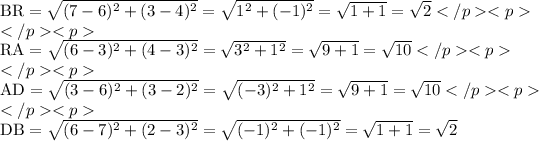
The lengths of the sides of KELY are:

`\text{KE}=√((2-0)^2+(11-9)^2)=√(2^2+2^2)=√(4+4)=√(8)=2√(2)</p><p>\\</p><p>\\\text{EL}=√((0-2)^2+(9-3)^2)=√((-2)^2+6^2)=√(40)=2√(10)</p><p>\\</p><p>\\\text{LY}=√((2-4)^2+(3-9)^2)=√((-2)^2+(-6)^2)=√(40)=2√(10)</p><p>\\</p><p>\\\text{YK}=√((4-2)^2+(9-11)^2)=√(2^2+(-2)^2)=√(8)=2√(2)`

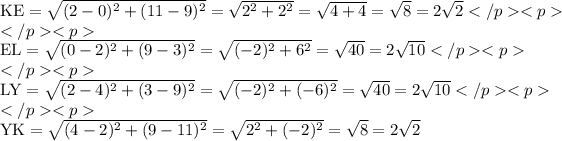
Each side of KELY is twice the length of the corresponding side on BRAD. This makes the ratio of the sides 2:1 and the figures are similar.