Question

You plant a rectangular rose garden along the side of your garage. You enclose 3 sides of the garden with 40 feet of fencing. The total area of the garden is 100 square feet. Find the possible dimensions of the garden.

Answer 1

Let's assume

length of rectangle =L

width of rectangle =W

You enclose 3 sides of the garden with 40 feet of fencing

so, we get

`L+2W=40`

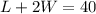
now, we can solve for L

`L=40-2W`

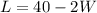
we know that

area of rectangle is

`A=L*W`

`100=L*W`

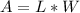
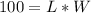
now, we can plug

`100=(40-2W)*W`

now, we can solve for W

`-2W^2+40W-100=0`

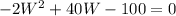
we can use quadratic formula

`W=(-40+√(40^2-4\left(-2\right)\left(-100\right)))/(2\left(-2\right))`

`W=(-40-√(40^2-4\left(-2\right)\left(-100\right)))/(2\left(-2\right))`

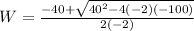
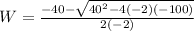
we can take anyone value ..because both are giving positive value

first dimensions:

`W=2.929`

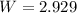
now, we can find L

`L=40-2*2.929`

`L=34.142`

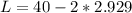
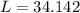
so, length is 34.142feet

width is 2.929 feet

Second dimensions:

`W=17.071`

now, we can find L

`L=40-2*17.071`

`L=5.858`

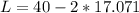
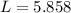
so, length is 5.858feet

width is 17.071 feet