Question

The mass of the Sun is 2 × 1030 kg, and the distance between Neptune and the Sun is 30 AU. What is the orbital period of Neptune in Earth years?

Answer 1

Kepler's third law states that, for a planet orbiting around the Sun, the ratio between the cube of the radius of the orbit and the square of the orbital period is a constant:

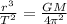
`(r^3)/(T^2)= (GM)/(4 \pi^2)` (1)
where
r is the radius of the orbit
T is the period
G is the gravitational constant
M is the mass of the Sun

Let's convert the radius of the orbit (the distance between the Sun and Neptune) from AU to meters. We know that 1 AU corresponds to 150 million km, so

`1 AU = 1.5 \cdot 10^(11) m`
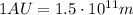
so the radius of the orbit is

`r=30 AU = 30 \cdot 1.5 \cdot 10^(11) m=4.5 \cdot 10^(12) m`

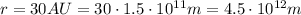
And if we re-arrange the equation (1), we can find the orbital period of Neptune:

`T=\sqrt{ (4 \pi^2)/(GM) r^3} = \sqrt{ (4 \pi^2)/((6.67 \cdot 10^(-11) m^3 kg^(-1) s^(-2) )(2\cdot 10^(30) kg))(4.5 \cdot 10^(12) m)^3 }= 5.2 \cdot 10^9 s`

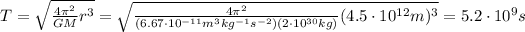
We can convert this value into years, to have a more meaningful number. To do that we must divide by 60 (number of seconds in 1 minute) by 60 (number of minutes in 1 hour) by 24 (number of hours in 1 day) by 365 (number of days in 1 year), and we get

`T=5.2 \cdot 10^9 s /(60 \cdot 60 \cdot 24 \cdot 365)=165 years`