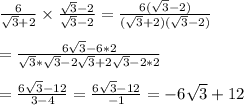Question

1. Simplify 2/radical 5

2. Simplify -11 radical 112
3. Simplify 17 radical 17 -9 radical 17
4. Simplify 6/ radical 3+2

Answer 1

1. (2√5)/5

2. -44√7

3. 8√17

4. -6√3+12

Explanation:

Answer 2

1. (2√5)/5
2. -44√7
3. 8√17
4. -6√3+12

For 1: Multiply the numerator and denominator by √5:

`(2)/(√(5))* (√(5))/(√(5))=(2√(5))/(5)`

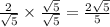
For 2: Simplify √112:
√112 = √(2*56) = √(2*2*28) = √(4*4*7) = 2*2√7 = 4√7
Now multiply by the -11 coefficient:
-11(4√7) = -44√7

For 3: Add the radicals as you would variables that are like terms.

For 4: Multiply by the conjugate. The conjugate of the denominator has the same values with the sign of the radical changed:

`(6)/(√(3)+2)* (√(3)-2)/(√(3)-2)=(6(√(3)-2))/((√(3)+2)(√(3)-2)) \\ \\=(6√(3)-6*2)/(√(3)*√(3)-2√(3)+2√(3)-2*2) \\ \\=(6√(3)-12)/(3-4)=(6√(3)-12)/(-1)=-6√(3)+12`