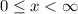Question

Jason made a payment of $1800 to his bank to clear his debts. He then deposited $1000 in his checking account at an annual interest rate of 6% compounded monthly. Jason made the following graph to relate the amount accumulated in his checking account in x number of years. What is the domain of the graph that Jason plotted?

Answer 1

Answer: The domain of the graph is
`0\eq x < \infty`

Explanation:

Here, the principal amount, P = $ 1000

Annual rate of interest r, = 6%

Thus, the total amount after x years on the account,

`A=1000(1+(6)/(100))^x=1000(1+0.06)^x=1000(1.06)^x`

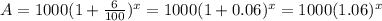
Hence, the function that shows the given situation,

`A(x)=1000(1.06)^x`

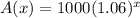
Since, the amount can not be negative and it must be less than infinite.

⇒
`0\leq A(x) < \infty`

⇒
`0\leq 1000(1.06)^x < \infty`

⇒
`0\leq x < \infty`

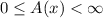
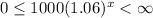
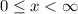
Since, the domain of A(x) = All possible value of x,

⇒ The domain of the function A(x) is
`0\leq x < \infty`

Answer 2

Jason made a payment of $1800 to his bank to clear his debts. He then deposited $1000 in his checking account at an annual interest rate of 6% compounded monthly. Jason made the following graph to relate the amount accumulated in his checking account in x number of years.

Here initial amount is 1000. the amount increases every year because the interest rate is 6% compounded monthly

From the graph we can see that the accumulated amount (y) increases as the number of years 'x' increases.

The number of years cannot be negative so we ignore negative values for x

Number of years starts at 0 and goes to infinity

So domain is 0 to infinity.