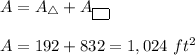Question

How would you find the area without the height of the triangle?

Answer 1

`\large\boxed{B.\ 1,024\ ft^2}`

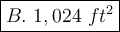
Explanation:

It's an equaliteral triangle. Therefore, the height divides the base in half.

Use the Pyhagorean theorem:

`h^2+\left((32)/(2)\right)^2=20^2`

`h^2+16^2=20^2`

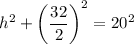
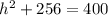`h^2+256=400` subtract 256 from both sides

`h^2=144\to h=√(144)\\\\h=12\ ft`

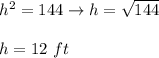
The formula of an area of a triangle:

`A_\triangle=(bh)/(2)`

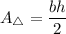
b - base

h - height

We have b = 32 ft and h = 12 ft. Substitute:

`A_\triangle=((32)(12))/(2)=(16)(12)=192\ ft^2`

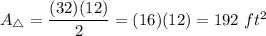
The formula of an area of a rectangle:

`A_{\boxed{\ }}=lw`

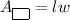
l - length

w - width

We have l = 32 ft and w = 26 ft. Substitute:

`A_{\boxed{\ }}=(32)(26)=832\ ft^2`

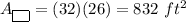
The area of the figure:

`A=A_\triangle+A_{\boxed{\ }}\\\\A=192+832=1,024\ ft^2`