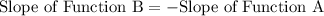Answer:
Option 4th is correct
Explanation:
Slope-intercept form:
The equation of line is given by:
y = mx+b
where, m is the slope and b is the y-intercept.
As per the statement:
The equation below represents Function A and the graph represents Function B:
Function A:
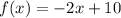
By slope intercept form:
Slope of the function A = -2
Function B:
Consider any two points from the given graph we have;
(0, -3) and (2, 1)
Using slope formula:
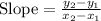
Substitute the given values we have;
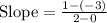
⇒
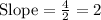
∴Slope of function B = 2
therefore,