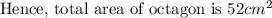Answer:
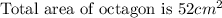
Explanation:
we have to find total area of octagon formed by removing four congruent right triangles from a rectangle.
First we have to find the the area of rectangle whose length and breadth are
Length=2+6+2=10 cm
Breadth=2+2+2=6 cm
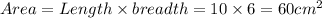
Area of 4 congruent right triangles are
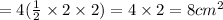
Area of octagon=area of rectangle-area of 4 triangles
=60-8=52 cm^2[/tex]