Question

The area of triangle ABC is 24 square centimeters. If B = 30° and a = 6 cm, what is the measure of side c?

Answer 1

The measure of side c is 16 cm.

Explanation:

Given information: Area of triangle ABC is 24 square centimeters.
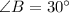`\angle B=30^(\circ)` and
`a=6cm`.

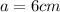Let the height of triangle ABC is

Draw a perpendicular on BC from A.

`\sin \theta=(perpendicular)/(hypotenuse)`

`\sin B=(AD)/(AB)`

`\sin 30=(h)/(c)`

`(1)/(2)=(h)/(c)`

`(1)/(2)* c=h`

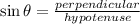
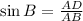
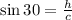
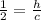
Therefore the height of triangle ABC is
`(1)/(2)* c`.

The area of triangle ABC is

`A=(1)/(2)* base* height`

`A=(1)/(2)* BC* AD`

`A=(1)/(2)* a* h`

`A=(1)/(2)* 6* ((1)/(2)* c)`

`A=3* ((c)/(2))`

`A=(3c)/(2)`

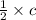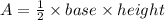
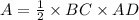
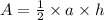
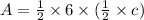
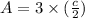
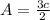
The area of triangle ABC is 24 square centimeters.

`24=(3c)/(2)`

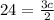
Multiply 2 both sides.

`48=3c`

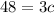
Divide both sides by 3.

`c=16`

Therefore the measure of side c is 16 cm.

Answer 2

we know that

the area of a triangle is
A=1/2 * a * c * sin (B°)
so
1/2 * 6 * c * sin (30°) = 24---------> 3*c*(1/2)=24--------> c=16 units

the answer is c=16 units