Question

if the current in a wire of a radio is 6.00 mA, how long would it take for 3.00 C of charge to pass a point in this wire

Answer 1

The current intensity is defined as the amount of charge that passes through a certain point in a certain time interval:

`I= (Q)/(\Delta t)`
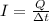
where
I is the current
Q the charge

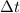
`\Delta t` is the time interval.

For the wire in our problem, the current is
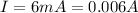
`I=6 mA=0.006 A` while the charge is
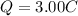
`Q=3.00 C`, so we can find the time interval by re-arranging the previous formula and using these data:

`\Delta t = (Q)/(I) = (3.00 C)/(0.006 A)=500 s`
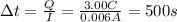
so, the charge takes 500 s to pass through a certain point of the wire.