Question

Billy is monitoring the exponential decay of a radioactive compound. He has a sample of the compound in a test tube in his lab. According to his calculations, the sample is decaying at a rate of 35% per hour. There are at least 72 grams of the sample remaining. Once the sample reaches a mass of 15 grams, Billy will continually add more of the compound to keep the sample size at a minimum of 15 grams. If R represents the actual amount of the sample remaining, in grams, and t represents the time in hours, then which of the following systems of inequalities can be used to determine the possible mass of the radioactive sample over time?

Answer 1

Formula for radioactive Decay is given by

`R_(0)= R(1-(S)/(100))^t`

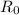`R_(0)`= Initial Population

R = Remaining population after time in hours

Rate of Decay = S % per hour

Initial Population = 72 grams

Final population = 15 grams

Rate of Decay = 35 % per hour

Substituting the values to get value of t in hours

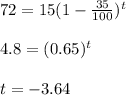`72=15(1-(35)/(100))^t\\\\ 4.8= (0.65)^t\\\\ t= -3.64`→→1 St expression

But taking positive value of t , that is after 3.64 hours the sample of 72 grams decays to 15 grams at the rate of 35 % per hour.

Now , it is also given that, Once the sample reaches a mass of 15 grams, Billy will continually add more of the compound to keep the sample size at a minimum of 15 grams.

Substituting these in Decay Formula

Final Sample = 15 gm

Starting Sample = 15 +k, where k is amount of sample added each time to keep the final sample to 15 grams.

Time is over 3.64 hours i.e new time = 3.64 + t

Rate will remain same i.e 35 % per hour.

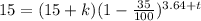`15=(15+k)(1-(35)/(100))^(3.64+t)`→→→ Final expression (Second) , that is inequalities can be used to determine the possible mass of the radioactive sample over time.

Answer 2

The required system of inequalities is,
`R\geq 72e^(-0.35t)` and
`R\geq 15`

Explanation:

We are given that,

The actual amount of sample remaining (in grams) = R.

Time (in hours) = t

The formula for the radioactive decay given by,
`N=N_(0)e^(-kt)`, where k = decay rate

As there are initially at-least 72 grams of the sample, which is decreasing at the rate of 35% = 0.35.

So,
`N_0=72` and k = 0.35

Thus, we get by substituting the values in the formula above,

`R\geq 72e^(-0.35t)`

Moreover, the minimum size of the sample is 15 grams. So, we have,

`R\geq 15`

Hence, the required system of inequalities is,

`R\geq 72e^(-0.35t)`

`R\geq 15`