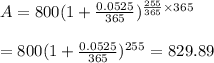Question

Calculate the account balance for $800 left on deposit for 255 days earning 5.25% compounded daily.

Answer 1

The value would be 829.89.

The formula we use is


`A=p(1+(r)/(n))^(nt)`,

where A is the total amount, p is the principal, r is the rate expressed as a decimal number, n is the number of times per year the interest is compounded, and t is the number of years.

We will use 800 for p; 5.25/100 = 0.0525 for r; 365 for n; and (255/365) for t (since it is not a full year):

`A=800(1+(0.0525)/(365))^{(255)/(365)*365} \\ \\=800(1+(0.0525)/(365))^(255)=829.89`