Answer:
The original length of the iron rod is approximately 572.189 meters.
Step-by-step explanation:
This is a case of linear expansion, which is defined by the following differential equation:
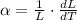 (1)
(1)
Where:
 - Linear expansion coefficient, measured in
- Linear expansion coefficient, measured in
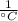 .
.
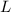 - Length of the element, measured in centimeters.
- Length of the element, measured in centimeters.
 - First derivative of the length of the element with respect to temperature, measured in centimeters per degree Celsius.
- First derivative of the length of the element with respect to temperature, measured in centimeters per degree Celsius.
If we assume that thermal deformation are small regarding the length of the element, then we simplify (1) in the following form:
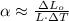

![L_(f) = L_(o)\cdot [1+\alpha\cdot (T_(f)-T_(o))]](https://img.qammunity.org/2022/formulas/physics/high-school/24xv67ypidjqyjnl9rtedbtp5aej8mlg8q.png) (2)
(2)
Where:
 ,
,
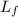 - Initial and final lengths of the element, measured in centimeters.
- Initial and final lengths of the element, measured in centimeters.
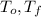 - Initial and final temperatures of the element, measured in degrees Celsius.
- Initial and final temperatures of the element, measured in degrees Celsius.
Given that brass has a higher coefficient of linear expansion, it is suppose that initial length is less than the initial length of the iron element. Then, we have the following system of linear equations:
Brass
![L = L_(o)\cdot [1+\alpha_(B)\cdot (T_(f)-T_(o))]](https://img.qammunity.org/2022/formulas/physics/high-school/pt5wg65v7tz7ddpd65a0xad9xwlth9q193.png) (3)
(3)
Iron
![L = (L_(o)+28)\cdot [1+\alpha_(I)\cdot (T_(f)-T_(o))]](https://img.qammunity.org/2022/formulas/physics/high-school/lc0ektteocono3kven0w5kad586l0tqkux.png) (4)
(4)
Where
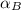 ,
,
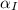 are coefficients of linear expansion of brass and iron, measured in
are coefficients of linear expansion of brass and iron, measured in
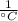 .
.
By equalizing (3) and (4), we have the following formula:
![L_(o) \cdot [1+\alpha_(B)\cdot (T_(f)-T_(o))] = (L_(o)+28)\cdot [1+\alpha_(I)\cdot (T_(f)-T_(o))]](https://img.qammunity.org/2022/formulas/physics/high-school/x23fvojdfzo01mh962izwnzf9uy9yjgus8.png)
![L_(o) \cdot (\alpha_(B)-\alpha_(I))\cdot (T_(f)-T_(o)) = 28\cdot [1+\alpha_(I)\cdot (T_(f)-T_(o))]](https://img.qammunity.org/2022/formulas/physics/high-school/o8pkuhvbn58l1f63t6axs342ied2dlub0l.png)
![L_(o) = (28\cdot [1+\alpha_(I)\cdot (T_(f)-T_(o))])/((\alpha_(B)-\alpha_(I))\cdot (T_(f)-T_(o) ))](https://img.qammunity.org/2022/formulas/physics/high-school/lxqzd31msix4g3gtwls77x57uy0mu5w00x.png)
If we know that
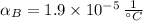 ,
,
 ,
,
 and
and
 , then the initial length of the iron rod is:
, then the initial length of the iron rod is:
![L_(o) = (28\cdot [1+\left(1.2* 10^(-5)\,(1)/(^(\circ)C) \right)\cdot (90\,^(\circ)C-20\,^(\circ)C)])/(\left(1.9* 10^(-5)\,(1)/(^(\circ)C)-1.2* 10^(-5)\,(1)/(^(\circ)C) \right)\cdot (90\,^(\circ)C-20\,^(\circ)C))](https://img.qammunity.org/2022/formulas/physics/high-school/69bkjoyy297ouau5lm9cu3wzppriwcj1oq.png)

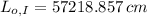
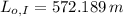
The original length of the iron rod is approximately 572.189 meters.