Question

Assume that men's weights are normally distributed with a mean of 172 lb and standard deviation of 29 lb (national health survey) if 81 men are randomly selected, find the probability that they have a mean weight less than 167 lb.

Answer 1

Answer: 0.0606

Explanation:

Given : The men's weights are normally distributed with a mean of 172 lb and standard deviation of 29 lb.

i.e.
`\mu=172` and
`\sigma=29`

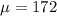and sample size : n= 81

Let x be a random variable that denotes the men's weights.

Formula :
`z=(x-\mu)/((\sigma)/(√(n)))`

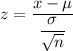
Then, the probability that they have a mean weight less than 167 lb will be :-

`P(x<167)=P((x-\mu)/((\sigma)/(√(n)))<(167-172)/((29)/(√(81))))\\\\=P(z<(-5)/((29)/(9)))\approx P(z<-1.55)\\\\=1-P(z<1.55)\ \ [\because\ P(Z<-z)=1-P(Z<z)]\\\\=1-0.9394\ \ [\text{Using z-value}]\\\\=0.0606`

Hence, the probability that they have a mean weight less than 167 lb = 0.0606