Question

What are the exact solutions of x2 = 5x + 2?

x = x equals 5 plus or minus the square root of thirty-three all over 2
x = x equals negative 5 plus or minus the square root of thirty-three all over 2
x = x equals 5 plus or minus the square root of seventeen all over 2
x = x equals negative 5 plus or minus the square root of seventeen all over 2

Answer 1

x^2 = 5x + 2
x^2 -5x -2 = 0
a = 1
b= -5
c= -2

x = [-b +- sq root (b^2 -4 ac)] / 2a
x = [--5 +- sq root (25 --8)] / 2a
x = [ 5 +- sq root (33)] / 2

Answer is "a"

Answer 2

Explanation:

The given equation is:

`x^2=5x+2`

which can be rewritten as:

`x^2-5x-2=0`

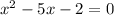
Now, since it is a quadratic equation, thus by using the discriminant method, we have

`x=\frac{-b{\pm}√(b^2-4ac)}{2a}`

`x=\frac{-(-5){\pm}√((-5)^2-4(1)(-2))}{2(1)}`

`x=\frac{5{\pm}√(25+8)}{2}`

`x=\frac{5{\pm}√(33)}{2}`

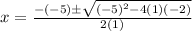
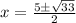
Thus, the value of x is equal to 5 plus or minus the square root of thirty-three all over 2, therefore option (A) is correct.