Question

What is the polynomial function of lowest degree with lead coefficient 1 and roots i, –2, and 2?

f(x) = x3 – x2 – 4x + 4
f(x) = x4 – 3x2 – 4
f(x) = x4 + 3x2 – 4
f(x) = x3 + x2 – 4x – 4

Answer 1

Option 2 is correct.

Explanation:

Given the roots of the polynomial function. we have to find the lowest degree polynomial with leading coefficient 1 and roots i, –2, and 2.

By complex conjugate root theorem which states that if P is the polynomial and a+ib is a root of P with a and b real numbers, then its complex conjugate a-ib is also a root of that polynomial P.

∴ -i is also the root of the polynomial function.

Hence, there are 4 roots of the given polynomial function f(x)

f(x) can be written as

`f(x)=(x+i)(x-i)(x+2)(x-2)`

`=(x^2-i^2)(x^2-2^2)`

`=(x^2+1)(x^2-4)`

`=x^4-4x^2+x^2-4`

`=x^4-3x^2-4`

Option 2 is correct.

Answer 2

We are given roots of a polynomial function : i, –2, and 2.

And leading coefficient 1 .

We need to find the polynomial function of lowest degree.

Please note: We have one root i, that is a radical root. And a radical always comes in pair of plug and minus sign.

Therefore, there would be another root -i.

So, we got all roots of the polynomial function : i, -i, -2, and 2.

For the given roots, we would have factors of the polynomial (x-i)(x+i)(x+2)(x-2).

Now, we need to multiply those factors to get the polynomial function.

`\mathrm{Expand}\:\left(x-i\right)\left(x+i\right):\quad x^2+1`

`\left(x+2\right)\left(x-2\right):\quad x^2-4`

`\left(x-i\right)\left(x+i\right)\left(x+2\right)\left(x-2\right)=\left(x^2+1\right)\left(x^2-4\right)`

`\mathrm{Expand}\:\left(x^2+1\right)\left(x^2-4\right)=x^4-4x^2+ \:x^2-\:4`

`=x^4-3x^2-4`

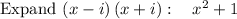
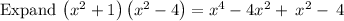
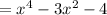
Therefore, correct option is 2nd option
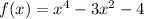`f(x)=x^4-3x^2-4`.