Answer: option A. Reduce the distance by a factor of 4.
Step-by-step explanation:
1) The electric potential energy, U is given by the formula
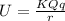
Where U is the electric potential energy, Q and q are the magnitude of the charges, and r is the distance between the charges.
2) That means that the electric potential energy is directly proportional to the product of the charges and inversely proportional to the distance between the two charges.
3) Therefore, withoud modifying the charges, when you reduce the distance, r, by a factor, the electric potential energy will be increased by the same factor.
Mathematically you can prove that in this way:
U₁ = KQq / r₁
U₂ = KQq / r₂
U₂ = 4 U₁ ⇒
KQq / r₂ = 4 KQq / r₁ ⇒ 1 / r₂ = 4 / r₁ ⇒ r₂ = r₁ / 4.
Which is that the distance is reduced by a factor of 4.