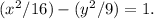Final answer:
The equation of the hyperbola with given foci and vertices is
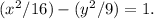 This is a horizontal hyperbola centered at the origin with a horizontal transverse axis.
This is a horizontal hyperbola centered at the origin with a horizontal transverse axis.
Step-by-step explanation:
The equation of a hyperbola can be determined using the distance between its foci and vertices. For the hyperbola with foci at (5, 0) and (-5, 0), and vertices at (4, 0) and (-4, 0), the focal distance c is 5 and the distance a, which is the distance from the center to the vertices, is 4. To find the equation of the hyperbola, we also need to determine b, which is the distance from the center to the co-vertices, using the relationship
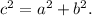 Since the foci and vertices lie on the x-axis, this is a horizontal hyperbola, and the equation has the form
Since the foci and vertices lie on the x-axis, this is a horizontal hyperbola, and the equation has the form
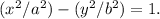
To find b, we calculate:
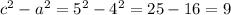 , so b = √9 = 3. Therefore, the equation of the hyperbola is
, so b = √9 = 3. Therefore, the equation of the hyperbola is
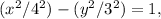 which simplifies to
which simplifies to