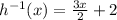Answer:
The inverse of the h(x) is
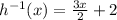 Explanation:
Explanation:
Given : Expression
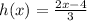
To find : The inverse of the expression ?
Solution :
Expression
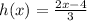
Let, h(x)=y then
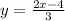
For inverse we replace the value of x and y and find the value of y in terms of x.
Replace the value of x and y,
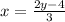
Solve for y by cross multiply,
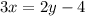
Adding 4 both side,
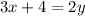
Dividing by 2 both side,
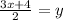
Therefore, The inverse of the h(x) is