Question

Find the angle between the hands of a clock at 5:15

A 60
B 67.5
C 75

Answer 1

The answer is B 67.5

Explanation:

I just did this problem and got it correct

Answer 2

Option B is correct.

67.5 degree

Explanation:

To find the angle between the hands of a clock.

Given that:

Hands of a clock at 5 : 15.

We know that:

A clock is a circle and it always contains 360 degree.

Since, there are 60 minutes on a clock.

`(360^(\circ))/(60 minutes) = 6^(\circ) per minutes`

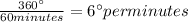
so, each minute is 6 degree.

The minutes hand on the clock will point at 15 minute,

then, its position on the clock is:

`(15) \cdot 6^(\circ) = 90^(\circ)`

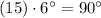
Also, there are 12 hours on the clock

⇒Each hour is 30 degree.

Now, can calculate where the hour hand at 5:00 clock.

⇒
`5 \cdot 30 =150^(\circ)`

Since, the hours hand is between 5 and 6 and we are looking for 5:15 then :

15 minutes is equal to
`(1)/(4)` of an hour

⇒
`150+(1)/(4)(30) = 150+7.5 = 157.5^(\circ)`

Then the angle between two hands of clock:

⇒
`\theta = 150.75 -90 = 67.5^(\circ)`

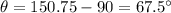
Therefore, the angle between the hands of a clock at 5: 15 is: 67.5 degree.