Question

Write the slope-intercept form of the line that passes through the points (6, 1) and (5, 4)

Answer 1

Remember that the general equation for slope-intercept form is y = mx + b, where m = the slope of the equation, b = the y intercept, and x and y are your variables (and the coordinate points on the graph).
First start by finding m, the slope. To find slope, use the equation:
`m = slope = ( y_(2) - y_(1) )/(x_(2)-x_(1))`
where
`x_(2)` and
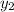
`y_(2)` are the x and y values of one coordinate point , and
`x_(1)` and
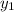
`y_(1)` are the x and y values of another coordinate point . Since we are given two coordinate points, that means we can find the slope using the slope equation.
Let's choose (6, 1) as your
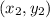
`(x_(2), y_(2))` point and (5, 4) as your
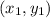
`(x_(1), y_(1))` point, but you can switch those if you want! That makes
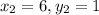
`x_(2) = 6, y_(2) = 1` and
`x_(1) = 5, y_(1) = 4`. Plug these values into the slope equation:

`slope = ( y_(2) - y_(1) )/(x_(2)-x_(1))\\ slope = (1-4)/(6-5) \\ slope = -3`

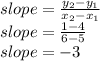
Now you know the slope of your line that passes through the points is m=-3. Plug that into your slope-intercept equation:
y = -3x +b

Finally you want to find b. To find b, just plug in one of your coordinate points and solve for b. I'll use (6,1), but you can use either one!

`y = -3x +b\\ 1 = -3(6) + b\\ 1 = -18 + b\\ b = 19`

Put b into your slope intercept equation to find your final equation of your line:
y = -3x + 19

The equation of your line is y = -3x + 19