Question

The orbital period of Jupiter is 11.86 years. What is its distance from the sun?

a. 3.7 AU
b. 5.2 AU
c. 37 AU
d. 52 AU

Answer 1

I just did the test and the answer is C.

Answer 2

The distance between the sun and the Jupiter is 5.2 AU.

Step-by-step explanation:

It is given that,

The orbital time period of Jupiter,
`T=11.86\ years`

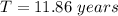
Since,
`1\ year=3.15* 10^7\ s`

`11.86\ year=3.74* 10^8\ s`

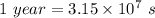
We need to find the distance from the sun. It can be calculated using Kepler's third law. It is mathematically given by :

`T^2=(4\pi^2)/(GM)a^3`

a = distance from sun

G universal gravitational constant

M is the mass of sun

`a^3=(T^2GM)/(4\pi^2)`

`a^3= ((3.74* 10^8\ s)^2* 6.67* 10^(-11)* 1.98* 10^(30))/(4\pi^2)`

`a=7.763* 10^(11)\ m`

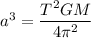
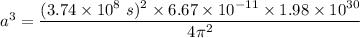
Since,
`1\ AU=1.496* 10^(11)\ m`

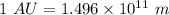
So,
`a=((7.763\cdot10^(11))/(1.496\cdot10^(11)))\ AU`

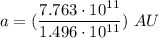
a = 5.189 AU

or

a = 5.2 AU

So, the distance from the sun is 5.2 AU. Hence, the correct option is (b).