Question

In two or more complete sentences, explain the theorem used in solving for the range of possible lengths of the third side, AB of triangle ABC

Answer 1

You can use the Pythagorean Theorem to find the length of the third side AB (Identified as "x" in the figure attached in the problem), which says that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the legs:
a² = b²+c²
As we can see the figure, the triangle does not have an angle of 90°, but it can be divided into two equal parts, leaving two triangles with a right angle. We already have the values of the hypotenuse and a leg in triangle "A" , so we can find the value of the other leg:
b = √(a²-c²) b = √(10²-4²) b = 9.16
With these values, we can find the hypotenuse in the triangle "B": x = √b²+c² x = √(9.16)²+(4)² x = 10

Answer 2

Explanation:

In triangle if two sides are known and included angle is known we can use cosine formula as follows:

Say in a triangle, sides a,b are known and also included angle C

Then the third side

`c^(2) =a^(2)+b^(2) -2abCos C`

Since all values on right side are known, we can find the third side c easily.

Case II:

If alternately two sides and one angle not included is known. i.e we know a,b and either angle A or B.

then to find third side we use sine formula.

`(a)/(sinA)=(b)/(sinB) =(c)/(sinC)`

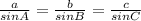
Using the above we can find the unknonwn side c easily.