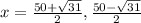Answer:
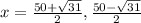 are zeroes of given quadratic equation.
are zeroes of given quadratic equation.
Explanation:
We have been a quadratic equation:

We need to find the zeroes of quadratic equation
We have a formula to find zeroes of a quadratic equation:
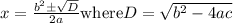
General form of quadratic equation is
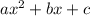
On comparing general equation with b given equation we get
a=2,b=-10,c=-3
On substituting the values in formula we get
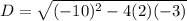
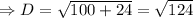
Now substituting D in
 we get
we get
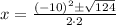
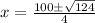
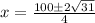
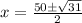
Therefore,