Question

What is the slope of the line that is perpendicular to a line whose equation is 3y = -4x + 2 ?

3/4

-3/4

4/3

-4/3

Answer 1

First let's put 3y = -4x + 2 into slope-intercept form. That way we can figure out the slope easier. Remember that slope-intercept from is: y = mx + b, where m = the slope and b = y-intercept.

To change 3y = -4x + 2 into that form, all we have to do is divide both sides by 3 to get y alone:

`3y = -4x + 2 \\ y = - (4)/(3) x + (2)/(3)`

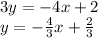
Since the "m" in slope-intercept form is the slope of the equation, that means
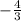
`- (4)/(3)` is the slope of
`y = - (4)/(3) x + (2)/(3)`.

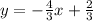
As a general rule to find a slope that is perpendicular, just find the negative inverse/reciprocal of your slope, meaning flip numerator and denominator of your slope and multiply by -1. Since your slope is
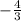
`- (4)/(3)`, the negative inverse/reciprocal of your slope (aka the perpendicular slope) would be:
`(3)/(4)`.

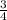
The answer is A) 3/4.

Answer 2

---------------------------------------------------
Rearrange to the format y = mx + b :
---------------------------------------------------
3y = -4x + 2
y = -4/3x + 2/3

---------------------------------------------------
Find Slope :
---------------------------------------------------
Slope = -4/3

---------------------------------------------------
Slope of the perpendicular line :
---------------------------------------------------
Perpendicular slope = 3/4 (negative reciprocal )

---------------------------------------------------
Answer: 3/4 (Answer A)
---------------------------------------------------