Answer:
x = 8,-2
Explanation:
First, complete the square on LHS (Left-Handed Side).
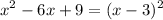
Make sure to recall the perfect square formula. Rewrite another equation with (x-3)² instead.
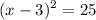
Square both sides of equation.
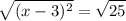
Because x² = (-x)² which means that it’s possible for x to be negative. Thus, write plus-minus beside √25 and cancel square of LHS.
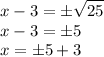
Therefore, x = 5+3 or x = -5+3
Thus, x = 8,-2
The method above is called completing the square method.