Question

James is driving to Madison from his home. His distance from Madison, f(x), in miles, changes as the number of hours, x, increases. The following graph represents James' distance from Madison.

Answer 1

1) The domain for function f is [ 0 , 4 ]

2) Intitial rate: r1=d/t1
d=320 miles
t1=4 hours
r1=(320 miles) / (4 hours)
r1=80 miles/hour

If James had driven 5 miles per hour faster for the entire drive to Madison:
Rate 2: r2=r1+5 miles/hour
r2=80 miles/hour + 5 miles/hour
r2=85 miles/hour

The domain of f would?
r2=d/t2
85 miles/hour=(320 miles)/t2
Solving for t2
(85 miles/hour) t2 = 320 miles
t2= (320 miles) / (85 miles/hour)
t2= 64/17 hours = 3.764705882 hours
t2=3.76 hours

The domain of f would be [ 0 , 64/17 ]

The domain of f would be reduced, because he would have driven at highest rate

Answer 2

From the graph, we can infer that the domain of the function is [0,4].

Remember that
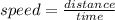
`speed= (distance)/(time)`. From the graph we can infer that
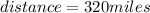
`distance=320miles` and
`time=4hours`, so Michael drove at a rate of
`s= (320)/(4) =80mi/h`.
Now, If Michel had driven 5 miles per hour faster for the entire ride, the new rate will be
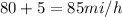
`80+5=85mi/h`. To find the new domain, we need to find the new time. since
`time= (distance)/(speed)`,
`time= (320)/(85) = (64)/(17)`.

We can conclude that the new domain will be
`[0, (64)/(17) ]`, or in decimal form:
`[0,3.76]`