Answer:
Explanation:
It is given that The area A of a sector of a circle is given by:
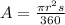
where where r is the radius of the circle and s is the angle measure(in degrees) of the sector.
Then, the equation for s can be obtained by rewriting the above given equation, thus
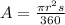
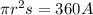
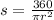
which is the required equation for s to find the angle measure given the radius and area of the circle.