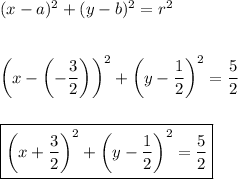Question

A circle has the order pairs (-1, 2) (0, 1) (-2, -1) what is the equation . Show your work.

Answer 1

We know that:


`(x-a)^2+(y-b)^2=r^2`

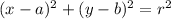
is an equation of a circle.

When we substitute x and y (from the pairs we have), we'll get a system of equations:


`\begin{cases}(-1-a)^2+(2-b)^2=r^2\\(0-a)^2+(1-b)^2=r^2\\(-2-a)^2+(-1-b)^2=r^2\end{cases}`

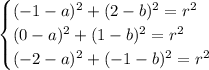
and all we have to do is solve it for a, b and r.

There will be:


`\begin{cases}(-1-a)^2+(2-b)^2=r^2\\(0-a)^2+(1-b)^2=r^2\\(-2-a)^2+(-1-b)^2=r^2\end{cases}\\\\\\ \begin{cases}1+2a+a^2+4-4b+b^2=r^2\\a^2+1-2b+b^2=r^2\\4+4a+a^2+1+2b+b^2=r^2\end{cases}\\\\\\ \begin{cases}a^2+b^2+2a-4b+5=r^2\\a^2+b^2-2b+1=r^2\\a^2+b^2+4a+2b+5=r^2\end{cases}\\\\\\`

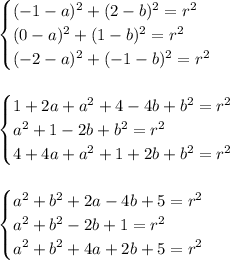
From equations (II) and (III) we have:


`\begin{cases}a^2+b^2-2b+1=r^2\\a^2+b^2+4a+2b+5=r^2\end{cases}\\--------------(-)\\\\a^2+b^2-2b+1-a^2-b^2-4a-2b-5=r^2-r^2\\\\-4a-4b-4=0\qquad|:(-4)\\\\\boxed{-a-b-1=0}`

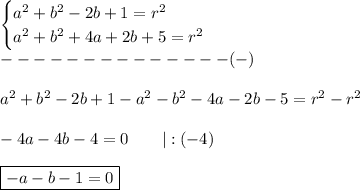
and from (I) and (II):


`\begin{cases}a^2+b^2+2a-4b+5=r^2\\a^2+b^2-2b+1=r^2\end{cases}\\--------------(-)\\\\a^2+b^2+2a-4b+5-a^2-b^2+2b-1=r^2-r^2\\\\2a-2b+4=0\qquad|:2\\\\\boxed{a-b+2=0}`

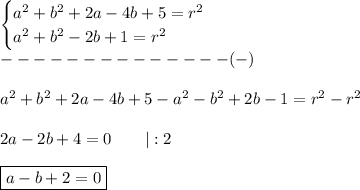
Now we can easly calculate a and b:


`\begin{cases}-a-b-1=0\\a-b+2=0\end{cases}\\--------(+)\\\\-a-b-1+a-b+2=0+0\\\\-2b+1=0\\\\-2b=-1\qquad|:(-2)\\\\\boxed{b=(1)/(2)}\\\\\\\\a-b+2=0\\\\\\a-(1)/(2)+2=0\\\\\\a+(3)/(2)=0\\\\\\\boxed{a=-(3)/(2)}`

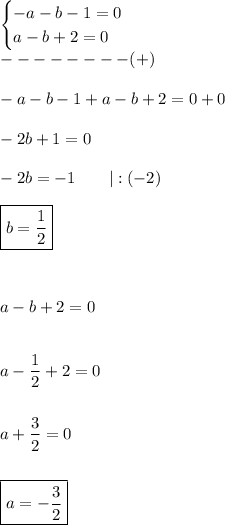
Finally we calculate
`r^2`:


`a^2+b^2-2b+1=r^2\\\\\\\left(-(3)/(2)\right)^2+\left((1)/(2)\right)^2-2\cdot(1)/(2)+1=r^2\\\\\\(9)/(4)+(1)/(4)-1+1=r^2\\\\\\(10)/(4)=r^2\\\\\\\boxed{r^2=(5)/(2)}`

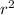
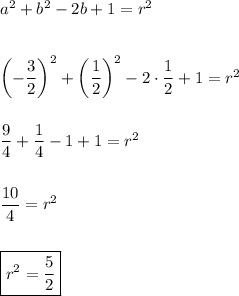
And the equation of the circle is:


`(x-a)^2+(y-b)^2=r^2\\\\\\\left(x-\left(-(3)/(2)\right)\right)^2+\left(y-(1)/(2)\right)^2=(5)/(2)\\\\\\\boxed{\left(x+(3)/(2)\right)^2+\left(y-(1)/(2)\right)^2=(5)/(2)}`