The table showing the conversion of angle measure in degrees to angles in gradients is attached below.
In order to find the slope we divide the difference of two y-coordinates (or dependent variable which in this case is gradient measure) by the difference of two respective x-coordinates (or independent variable which in this case is degree measure).
For finding the slope we will use the first and the last point given in the table. So, the slope m will be given by:
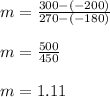 So rounding of to nearest hundredth, the slope of line representing the conversion of degrees to gradients is 1.11
So rounding of to nearest hundredth, the slope of line representing the conversion of degrees to gradients is 1.11