Question

What is the interquartile range (IQR) of this data set?

2,6,7,11,15,16,17

a, 10
b,9
c,7
d,15

Answer 1

The IQR is the difference between 3rd and 1st quartile. So we have to find the quartiles to answer the question.

2,6,7,11,15,16,17

1st Q: 6
2nd Q: 16
Median (Middle number in data) : 11

IQR: 16 - 6 = 10
IQR: 10

Answer 2

The interquartile range (IQR) is 10.

Explanation:

As you have an odd and ordered dataset, first of all you have to choose the median of the dataset, that is the number that is just in the center, in this case the median is the number 11 (Please she the figure below).

Now you have one lower half with the numbers 2, 6, 7 and an upper half with the numbers 15, 16, 17

As you can see in the figure, you have to find the median for these lower and upper halfs, so you have:

`Q_(1)=6`

`Q_(3)=16`

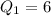
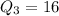
Now you can find the interquaritle range that is:

`IQR=Q_(3)-Q_(1)`

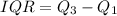
IQR = 16 - 6

IQR = 10