Question

The function f(x) = x2 is translated 7 units to the left and 3 units down to form the function g(x). Which represents g(x)?

g(x) = (x − 7)2 − 3
g(x) = (x + 7)2 − 3
g(x) = (x − 3)2 − 7
g(x) = (x − 3)2 + 7

Answer 1

i think its
g(x) = (x + 7) 2 - 3
hope this helps,
QueenofLovers123

Answer 2

`g(x)=(x+7)^2-3`

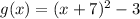
2nd option is correct.

Explanation:

The parent function is
`f(x)=x^2`

We can use below transformation rule:

• Whenever, we translate parent function f(x) by 'a' units left then we can add "a" the x value.Thus equation of f(x) becomes f(x+a)
• When we shift f(x) down by 'a' units then equation of f(x) becomes f(x)-a

Now, first of all this function is translated 7 units to the left.

Hence, the equation becomes
`g(x)=(x+7)^2`

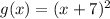
Finally, f(x) shifts down by 3 units then equation becomes

`g(x)=(x+7)^2-3`

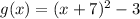
2nd option is correct.